15 МАР
2023
Математик ЗабГУ вывел закон симметрии в процессах теплообмена
Профессор Забайкальского государственного университета, доктор физико-математических наук Святослав Евгеньевич Холодовский разработал математический метод решения задач, моделирующих тепловые потоки (от более нагретых к менее нагретым зонам) в телах, содержащих слабопроницаемую пленку внутри или на границе. Такие пленки широко применяются при теплоизоляции зданий, в нанотехнологиях, при производстве композитных материалов и других областях. На основании полученных формул ученый вывел закон влияния пленок на процессы теплообмена в различных телах.
Закон, названный законом симметрии, формулируется следующим образом. Рассматривается произвольный тепловой поток в теле без пленки. Если в это тело внести пленку, разделяющую тело на две зоны, то температура в зоне, где расположены источники тепла, будет повышаться, а в другой зоне – понижаться. При этом оказалось, что температура будет повышаться и понижаться в симметричных относительно пленки точках тела на одинаковую величину. Выведена формула, выражающая указанное повышение (понижение) температуры в различных точках в зависимости от толщины и теплопроводности пленки.
Показано, что на пленке температура имеет разрыв (скачок), при этом скорость теплового потока сквозь пленку пропорциональна скачку температур на сторонах пленки, т.е. чтобы тепловому потоку «прорвать» слабопроницаемую пленку нужно на ее сторонах поддерживать определенную разность температур.
Полученные результаты позволяют глубже понять законы природы в процессах теплообмена. На практике полученный закон, в частности, позволит по известным параметрам теплоизолятора рассчитывать потери тепла при теплоизоляции зданий, труб горячего водоснабжения и т.д.
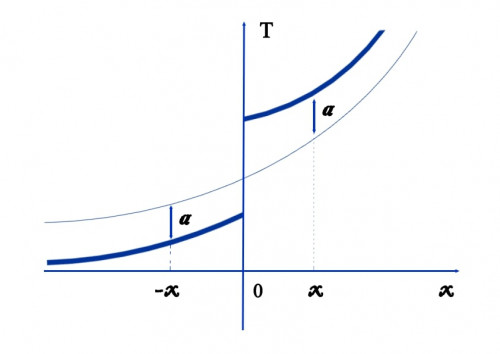
На рисунке изображен график температуры в теле без пленки (тонкая линия) и график этого же теплового потока (жирная линия) при наличии пленки . На пленке температура имеет разрыв – скачок. Из рисунка видно, что наличие пленки повышает температуру в области справа и понижает температуру в области слева по сравнению с температурой без пленки, при этом повышение и понижение температуры в симметричных относительно пленки точках и происходит на одинаковую величину.
Статья опубликована в математическом журнале «Дифференциальные уравнения», 2022, том 58, № 4, с. 509-518.
https://sciencejournals.ru/view-article/?j=deqrus&y=2022&v=58&n=4&a=DeqRus_2204007Kholodovskii)

